Nel mondo della meccanica, pochi sistemi sono tanto semplici quanto efficaci come l’accoppiamento cremagliera–pignone. Questo meccanismo, apparentemente elementare, è in realtà alla base di moltissime applicazioni industriali e quotidiane, grazie alla sua capacità di trasformare un moto rotatorio in un moto lineare – o viceversa – in modo diretto, preciso e affidabile.
Cos’è una cremagliera e a cosa serve
La cremagliera è un ingranaggio lineare che lavora in accoppiamento con una ruota dentata, detta pignone. Quando il pignone ruota, i denti ingranano con quelli della cremagliera generando uno spostamento rettilineo; viceversa, un movimento lineare della cremagliera può mettere in rotazione il pignone.
Questa caratteristica rende il sistema estremamente versatile e lo ritroviamo in molte applicazioni:
- Settore ferroviario: nelle linee con forti pendenze, dove la sola aderenza ruota–rotaia non è sufficiente, la cremagliera consente al treno di “arrampicarsi” su inclinazioni molto elevate in totale sicurezza.
- Settore automotive: lo sterzo a cremagliera e pignone è lo standard nelle automobili moderne, perché permette di convertire la rotazione del volante in uno spostamento laterale preciso delle ruote.
- Automazione e industria: macchine utensili, sistemi di posizionamento, assi lineari e macchinari speciali utilizzano cremagliere per movimentare carichi con precisione e ripetibilità.
Com’è fatta una cremagliera?
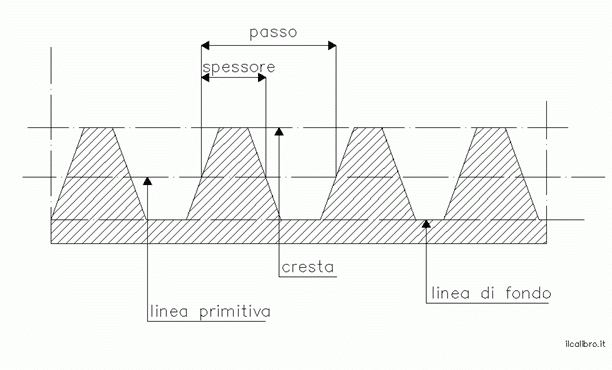
Dal punto di vista costruttivo, la cremagliera è una barra metallica dentata, generalmente in acciaio, con denti a profilo trapezoidale (normalmente evolvente, come negli ingranaggi cilindrici).
Per identificarla e sceglierla correttamente, è fondamentale conoscere alcuni parametri geometrici.
Il passo P
Il passo P è la distanza lineare tra un punto di un dente e lo stesso punto del dente successivo sulla cremagliera. È uno dei parametri principali perché determina direttamente la dimensione dei denti.
Il modulo: il parametro chiave
Come per qualsiasi ruota dentata, anche per la cremagliera il parametro più importante è il modulo.
Il modulo m è definito come:
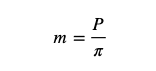
Il modulo rappresenta una misura normalizzata della dimensione del dente ed è fondamentale per garantire la compatibilità tra pignone e cremagliera: due elementi possono ingranare correttamente solo se hanno lo stesso modulo.
Non a caso, nei cataloghi tecnici il modulo è sempre indicato ed è uno standard di riferimento nella progettazione meccanica.
Circonferenza e raggio della primitiva
Un altro concetto importante è quello di circonferenza primitiva.
Per il pignone, la circonferenza primitiva C si calcola come:
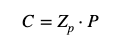
dove Zp è il numero di denti del pignone.
Da questa possiamo ricavare il raggio della primitiva R:
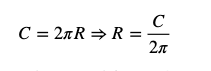
Il raggio della primitiva è un parametro chiave perché entra direttamente nel calcolo delle forze trasmesse tra pignone e cremagliera.
Come dimensionare una cremagliera
Il dimensionamento di una cremagliera dipende essenzialmente da tre fattori:
- Lunghezza necessaria
- Forza richiesta
- Velocità di spostamento
Lunghezza della cremagliera
La lunghezza L della cremagliera necessaria si calcola a partire dal numero di giri del pignone:
dove:
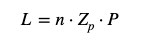
- è il numero di giri del pignone,
- il numero di denti,
- il passo.
Forza trasmessa sulla cremagliera
Per garantire lo spostamento richiesto, il pignone deve trasmettere una forza lineare sufficiente. Questa forza è legata alla coppia applicata al pignone dalla relazione:
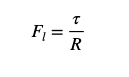
dove:

Da questa formula emerge un concetto fondamentale:
a parità di coppia applicata, più piccolo è il raggio della primitiva, maggiore sarà la forza lineare trasmessa alla cremagliera.
Il raggio della primitiva può essere ridotto:
- diminuendo il numero di denti del pignone;
- diminuendo il passo (e quindi il modulo).
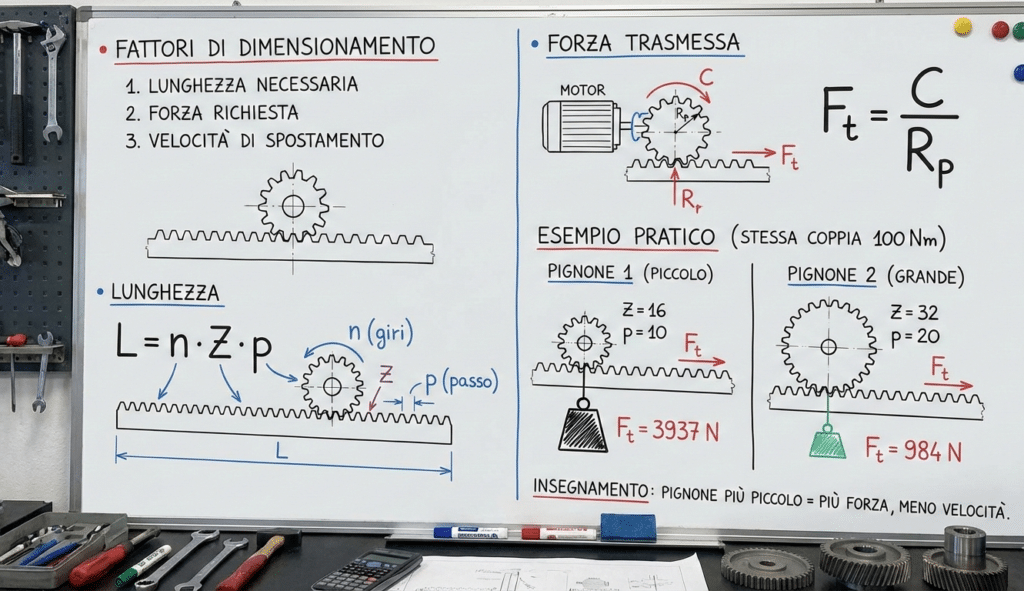
Esempio pratico
Consideriamo due pignoni a cui viene applicata la stessa coppia di 100 Nm:
Pignone 1

Pignone 2

Cosa ci insegna questo esempio
A parità di coppia applicata, il pignone più piccolo trasmette una forza circa quattro volte maggiore rispetto a quello più grande. Questo lo rende ideale per applicazioni in cui è richiesta molta forza.
Tuttavia, c’è un compromesso importante da considerare:
un pignone più piccolo deve compiere un numero maggiore di giri per percorrere la stessa distanza lineare di un pignone più grande. In altre parole, più forza significa meno velocità, e viceversa.
Questo equilibrio tra forza e velocità è fondamentale nella progettazione delle macchine CNC.
Conclusioni
Il sistema cremagliera–pignone è un perfetto esempio di come la meccanica trasformi concetti semplici in soluzioni estremamente efficaci.
Dimensionare correttamente una cremagliera significa trovare il giusto equilibrio tra forza, velocità e precisione, scegliendo con attenzione modulo, passo e numero di denti del pignone.
Comprendere questi parametri è il primo passo per progettare sistemi affidabili, efficienti e adatti all’applicazione specifica – ed è proprio qui che l’ingegneria meccanica mostra tutta la sua eleganza.
Richiedi una consulenza tecnica per scoprire come LabMec integra questi principi nella progettazione delle sue macchine.
Labmec, Macchine CNC







